Ejercicio de torsión 03
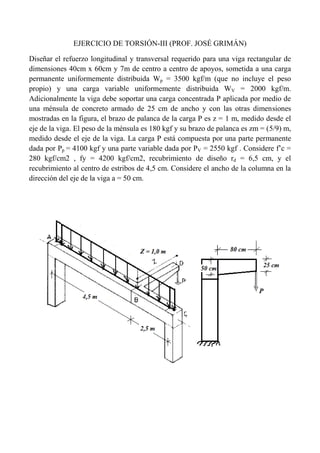
- 1. EJERCICIO DE TORSIÓN-III (PROF. JOSÉ GRIMÁN) Diseñar el refuerzo longitudinal y transversal requerido para una viga rectangular de dimensiones 40cm x 60cm y 7m de centro a centro de apoyos, sometida a una carga permanente uniformemente distribuida Wp = 3500 kgf/m (que no incluye el peso propio) y una carga variable uniformemente distribuida WV = 2000 kgf/m. Adicionalmente la viga debe soportar una carga concentrada P aplicada por medio de una ménsula de concreto armado de 25 cm de ancho y con las otras dimensiones mostradas en la figura, el brazo de palanca de la carga P es z = 1 m, medido desde el eje de la viga. El peso de la ménsula es 180 kgf y su brazo de palanca es zm = (5/9) m, medido desde el eje de la viga. La carga P está compuesta por una parte permanente dada por Pp = 4100 kgf y una parte variable dada por PV = 2550 kgf . Considere f’c = 280 kgf/cm2 , fy = 4200 kgf/cm2, recubrimiento de diseño rd = 6,5 cm, y el recubrimiento al centro de estribos de 4,5 cm. Considere el ancho de la columna en la dirección del eje de la viga a = 50 cm.
- 2. SOLUCIÓN: 1. Análisis de cargas: Datos: Sobre la viga: Se determina el peso propio por unidad de longitud de viga. Wconcreto =2400 kgf/m3 , Peso permanente wpl = 0,40·0.60·2400 = b = 0,4 h = 0,6 WC = 2400 wp = 576 kgf/m Cargas mayoradas aplicadas a la viga: Carga distribuida mayorada: Carga distribuida permanente total: 3500 + 576 = 4076 kgf/m Carga distribuida variable: 2000 kg/m wuv1 = 1,4·4076 = factor = 1,4 wp 4076 kgf/m wu1 = 5706,4 kgf/m wuv2 = 1,2·4076+1,6·2000 = factor cp = 1,2 factor cv = 1,6 wpl = 4076 wvl = 2000 wuL2 = 8091,2 kgf/m Carga distribuida mayorada se toma igual a wu = 8091,2 kgf/m Carga concentrada mayorada: Puv1 = 1,4·4280 = 5992 kgf Puv2 = 1,2·4280+1,6·2550 = 9216 kgf Se toma como carga concentrada mayorada igual a Pu = 9216 kgf
- 3. Diagrama de corte y diagrama de torsión: Se tiene conocido: wu = 8091,2 kgf/m, Pub = 9216 kgf, Se determina el torque concentrado en B, Tub: Se tiene Tbp = 4100·1 + (5/9)·180 = 4200 kgf-m Se tiene Tbv = 2550·1 = 2550 kgf-m El momento de torsión concentrado mayorado es: Tub = 1,2·4200 + 1,6·2550 = 9120 kgf-m De un programa de elementos finitos para análisis estructural se obtiene: Mc = 31079,53 kgf-m y Ma = 30168,1 kgf-m. Tc = 5443,8 kgf-m y Ta = 3676,2 kgf-m Vc = 34373,98 kgf y Va = 31480,42 kgf
- 4. Se determina el diagrama de fuerza cortante: 0 ≤ x ≤ 2,5 m, V = 34373,98 – 8091,2·x En x = 2,5 m, V(x = 2,5 m) = 34373,98 – 8091,2·2,5 = 14145,98 kgf Luego de la carga aplicada, V(x > 2,5 m) =14145,98 - 9216 = 4929,98 kgf 2,5 m ≤ x ≤ 7 m, V = 4929,98 – 8091,2·x En x = 7 m, V(x = 7 m) = 4929,98 – 8091,2·4,5 = -31480,42 kgf Diagrama de fuerza cortante Se determina el diagrama de torsión: Se adoptará como convención que un vector de momento torsión actuante en un punto, que apunte hacia la izquierda genera un salto positivo en el diagrama de torsión, y un vector torsión actuante que apunte a la derecha, genera entonces un salto negativo en el diagrama de torsión.
- 5. Considerando d = 53,5 cm y como el ancho de los apoyos es a = 50 cm, las secciones críticas para corte y para torsión quedan a (53,5 + 50/2) = 78,5 cm, medidos desde el centro del apoyo. Estudiamos primero el lado CB. Vucrit = 34373,98 – 8091,2·0,785 = Vu = 34373,98 kgf wu = 8091,2 kgf/m x secc crit = 0,785 m Vucrit = 28022,39 kgf Tucrit = 5443,8 kgf·m Se chequea si 𝑻 𝒖 ≤ 𝝓 ∙ 𝟎, 𝟐𝟕 ∙ √ 𝒇′ 𝒄 ∙ 𝑨 𝒄𝒑 𝟐 𝑷 𝒄𝒑 (16.6). Si se cumple entonces se pueden despreciar los efectos de la torsión. Acp = 40·60= b = 40 cm h = 60 cm Acp = 2400 cm2 Pcp = 2·(40+60) = b = 40 cm h = 60 cm Pcp = 200 cm
- 6. 𝑻 𝒖 ≤ 𝝓 ∙ 𝟎, 𝟐𝟕 ∙ √ 𝒇′ 𝒄 ∙ 𝑨 𝒄𝒑 𝟐 𝑷 𝒄𝒑 = 𝟎, 𝟕𝟓 ∙ 𝟎, 𝟐𝟕 ∙ √ 𝟐𝟖𝟎 ∙ 𝟐𝟒𝟎𝟎 𝟐 𝟐𝟎𝟎 = 975,88 kgf·m Como Tu crit = 5443,8 kgf·m, > 975,88 kgf·m, se debe considerar la torsión. Estudiando la porción AB, con origen en A hacia B. Vucrit = -31480,42 + 8091,2·0,785 = Vu = -31480,42 kgf wu = 8091,2 kgf/m x secc crit = 0,785 m Vucrit = -25128,83 kgf Tu crit = -3676,2 kgf-m Pero para efecto de los cálculos siguientes, estos valores se consideran en valor absoluto. Considerando que se tiene la misma sección transversal, se tiene que como Tu crit = 3676,2 kgf·m, > 975,88 kgf·m, se debe considerar la torsión en el diseño de la porción AB. Se debe tener en cuenta que tenemos en este caso una torsión primaria, por lo cual los valores de Tu no se deben reducir. Antes de diseñar el refuerzo a torsión se debe verificar que la sección cumple con la ecuación: Se calcula Aoh y Ph considerando las dimensiones de la viga: xo = 40 – 2·4,5 = 31 cm yo = 60 – 2·4, 5 = 51 cm Aoh = xo·yo = 31·51 = 1581 cm^2
- 7. Ph = 2·(xo +yo) = 2·( 31+51) Ph = 164 cm Se chequea entonces la fórmula 11.21 de la Norma 1753-06 √( 28022,39 40 · 53,5 ) 2 + ( 5443,8 ∙ 100 · 164 1,7 · 15812 ) 2 ≤ 0,75 ∙ 2.7 ∙ √280 24,76 < 33,88 kgf/cm2 Como la relación se cumple se continúa con el diseño, si no fuera así se debería aumentar la sección de concreto. Esta misma relación nos permite concluir que para el lado AB también se cumple porque Vu crit y Tu crít del lado AB son menores a los considerados aquí. Diseño por torsión del lado CB: Como se cumple que 𝑻 𝒖 ≤ 𝝓 ∙ 𝟎, 𝟐𝟕 ∙ √ 𝒇′ 𝒄 ∙ 𝑨 𝒄𝒑 𝟐 𝑷 𝒄𝒑 se considera la torsión Se calcula el acero transversal por torsión: 𝐴 𝑡 𝑠 = 𝑇𝑢 𝜙⁄ 2 ∙ 𝐴 𝑜 ∙ 𝑓𝑦𝑣 ∙ 𝑐𝑡𝑔 𝜃 Asumiendo θ = 45°, Ao = 0.85·Aoh = 0.85·1581= 1343,85 cm2 𝐴 𝑡 𝑠 = 5443,8·100 0.75⁄ 2∙1343,85∙4200∙𝑐𝑡𝑔 45° = 0,0643 cm^2/cm
- 8. Entonces 2𝐴 𝑡 𝑠 = 2 ∙ 0,0643 = 0,1286 cm^2/cm Se calcula el acero transversal por cortante: Se chequea si 𝑉𝑢 ≥ 𝜙 ∙ 𝑉𝑐 : Se calcula ϕ·Vc = 𝜙 · 0,53 · √𝑓′𝑐 · 𝑏 𝑤 · 𝑑 = 0,75 · 0,53 · √280 · 40 · 53,5 = 𝜙·Vc = 14234,097 kgf Como Vu = 28022,39 kgf es mayor que 𝜙Vc = 14234,097 kgf , se requiere acero transversal por corte, se calcula el acero transversal por corte: Se calcula Vs = 𝑉 𝑢 𝑐𝑟𝑖𝑡−𝜙𝑉𝑐 𝜙 = 28022,39−14234,097 0,75 = 18384,3907 kgf Se chequea con Vsmax = 2.1 · √𝑓′𝑐 · 𝑏 𝑤 · 𝑑 = 2.1 · √280 · 40 · 53,5 = 𝑉𝑠𝑚𝑎𝑥 = 75199,0032 kgf Como Vs es menor que Vsmax , se continua con el diseño, no se requiere aumentar la sección. Calcula el acero necesario por cortante: 𝐴 𝑣 𝑠 = 𝑉𝑢 𝜙⁄ −𝑉𝑐 𝑓𝑦𝑣·𝑑 = 28022,39 0,75⁄ −14234,097 0,75⁄ 4200·53,5 = 0,082 cm^2/cm Se compara con Av / s min = 0.20·√𝑓′𝑐·𝑏 𝑤 𝑓𝑦𝑣 ≥ 3.5·𝑏 𝑤 𝑓𝑦𝑣 𝐴 𝑣 𝑠 min = 0,20·√280·40 4200 = 0,032 cm^2/cm 3,5·40 4200 = 0,0333 cm^2/cm Se debe colocar 𝐴 𝑣 𝑠 = 0,082 cm2 /cm Considerando torsión + corte, se calcula el acero transversal total: 𝐴 𝑣𝑡 𝑠 = 𝐴 𝑣 𝑠 + 2 · 𝐴 𝑡 𝑠 = 0.082 + 0,1286 = 0,2106 cm2/cm Se chequea que 𝐴 𝑣𝑡 𝑠 ≥ 3,5·𝑏 𝑤 𝑓𝑦𝑣 ⟹ se cumple 0,2106 > 0,0333
- 9. Se asume el área de estribos como # 4 de dos ramas: Av = 2·1,27 = 2,54 cm2 = 𝑠 = á𝑟𝑒𝑎 𝑑𝑒 𝑙𝑎𝑠 𝑑𝑜𝑠 𝑟𝑎𝑚𝑎𝑠 𝐴 𝑣𝑡 𝑠⁄ = 2,54 0,2106 = 12,06 cm Se calculan las separaciones máximas para torsión y para cortante y se coloca la más exigente: Por torsión 𝑠 𝑚𝑎𝑥 𝑡𝑜𝑟𝑠𝑖ó𝑛 =≤ {𝑃ℎ 8⁄ ; 30 𝑐𝑚} = {164 8⁄ = 20,5 𝑐𝑚 ; 30 𝑐𝑚} = 20,5 𝑐𝑚 Por cortante: Se chequea si Vs es menor que 1,06 · √𝑓′𝑐 · 𝑏 𝑤 · 𝑑 = 37957,5921 kgf Se cumple, entonces smax = d/2 o 60 cm (Para ND1) 𝑠 𝑚𝑎𝑥 𝑐𝑜𝑟𝑡𝑒 =≤ {0,5 · 𝑑 ; 60 𝑐𝑚; 5 · 𝐴 𝑣𝑡 · 𝑓𝑦𝑣 𝑏 𝑤 · √𝑓′𝑐 ; 𝐴 𝑣𝑡 · 𝑓𝑦𝑣 3,5 · 𝑏 𝑤 } = 𝑠 𝑚𝑎𝑥 𝑐𝑜𝑟𝑡𝑒 =≤ {0,5 · 53,5 ; 60 𝑐𝑚; 5 · 2,54 · 4200 40 · √280 ; 2,54 · 4200 3,5 · 40 } = 0,5·53,5 = 26,75 cm 5·2,54·4200 40·√280 = 79,69 cm 2,54·4200 3,5·40 = 76,20 cm Separación elegida es : s = 12 cm. El primer estribo se colocará a 5 cm de la cara del apoyo, y los estribos siguientes a cada 12 cm, hasta donde sea necesario. El refuerzo por torsión deja de ser necesario en el punto donde 𝑻 𝒖 = 𝝓 ∙ 𝟎, 𝟐𝟕 ∙ √ 𝒇′ 𝒄 ∙ 𝑨 𝒄𝒑 𝟐 𝑷 𝒄𝒑 = 𝟎, 𝟕𝟓 ∙ 𝟎, 𝟐𝟕 ∙ √𝟐𝟖𝟎 ∙ 𝟐𝟒𝟎𝟎 𝟐 𝟐𝟎𝟎 = = 975,88 kgf·m Como en cualquier punto de la viga, el momento de torsión Tu es mayor que este valor del umbral de torsión, entonces se requiere refuerzo por torsión en toda la viga.
- 10. Hacemos una tabla para considerar el efecto de las variaciones en Vu y Tu, en las separaciones de los estribos: x (m) Vu Tu 2At/s Av/s 2At/s + Av/s s (cm) 0,785 28022,39 5443,8 0,1286 0,0818 0,21041745 12,0712424 1 26282,782 5443,8 0,1286 0,0715 0,20009489 12,693977 1,5 22237,182 5443,8 0,1286 0,0475 0,17608896 14,4245271 1,9 19000,702 5443,8 0,1286 0,0283 0,15688421 16,1902841 2,2 16573,342 5443,8 0,1286 0,0139 0,14248065 17,8269816 2,49 14226,894 5443,8 0,1286 0,0000 0,12855721 19,7577402 2,5 14145,982 5444,8 0,1286 0,0000 0,12862358 19,747546 Se puede observar en la tabla a partir de 1,90 m desde el eje del apoyo se pueden colocar los estribos a cada 16 cm con el fin de reducir el número de estribos necesarios. Observe que en x = 2,49 m, Vu es casi igual a 𝜙Vc = 14234,097 kgf, por lo cual la cantidad (Av / s) es prácticamente cero, es decir es este punto, teóricamente no se requiere refuerzo por cortante. Se colocaran estribos cerrados #4, el primero a 5 cm desde la cara de apoyo, luego 14 estribos a cada 12 cm hasta una distancia de 1,98 m desde el eje del apoyo. Luego 4 estribos a cada 16 cm, con lo cual se llega hasta una distancia de 2,62 m. En total 19 estribos como refuerzo transversal por corte y torsión. Se calcula ahora el acero longitudinal. Se tiene 𝐴 𝑡 𝑠 = 5443,8·100 0.75⁄ 2∙1343,85∙4200∙𝑐𝑡𝑔 45° = 0,0643 cm^2/cm 𝑨𝒍 = ( 𝑨𝒕 𝒔 ) · 𝒑 𝒉 · ( 𝒇 𝒚𝒗 𝒇 𝒚𝒍 ) · 𝑪𝒕𝒈 𝟐 𝜽 ≥ 𝟏, 𝟑𝟑 · √𝒇′ 𝒄 · 𝑨 𝒄𝒑 𝒇 𝒚𝒍 − ( 𝑨𝒕 𝒔 ) · 𝒑 𝒉 · ( 𝒇 𝒚𝒗 𝒇 𝒚𝒍 ) 𝑨𝒍 = (𝟎, 𝟎𝟔𝟒𝟑) · 𝟏𝟔𝟒 · (𝟏) · 𝟏 𝟐 = 10,55 cm^2 Para calcular el Al min, At/s no debe ser menor que 1,75bw / fy =1,75·40/4200 =0,017, cumple: 𝟏,𝟑𝟑·√𝟐𝟖𝟎·𝟐𝟒𝟎𝟎 𝟒𝟐𝟎𝟎 − (𝟎. 𝟎𝟔𝟒𝟑) · 𝟏𝟔𝟒 · (𝟏) = 2,1720324 cm^2 Se cumple con Al > Al mín.
- 11. Si se divide Ph entre los 30 cm de separación máxima que deben tener entre sí las barras de refuerzo longitudinal por torsión, se obtiene aproximadamente el número de barras necesarias. No. Barras = 164 / 30 = 5,47 , se consideran 6 barras. El diámetro debe ser mayor que 0,042·s = 0,042·12 =0,504 cm, pero no menor que la #3, es decir el diámetro =(3/8)·2,54 =0,953 cm. Consideremos 6 barras: el área de una barra será aproximadamente: 10,55 / 6 = 1,76 cm2 , lo cual se satisface con barras #5, con área Ab= 1,98 cm2 . Diseño por flexión de la sección rectangular: 40 x 60: Momento flexionante: En máximo en el apoyo C: 𝑀𝑐 = 31079,53 𝑘𝑔𝑓 − 𝑚 En el tramo, el punto donde el cortante es cero es en: 𝑥 𝑚 = 31480,42 8091.2 = 3,891 𝑚, medidos desde A hacia B. Entonces el momento máximo en el tramo es: 𝑀 𝑚−𝑡𝑟𝑎𝑚𝑜 = 31480,42 · 3,891 − 30168,1 − 8091,2∙3,8912 2 = 31072,31 kgf-m Se dimensiona la sección para el momento mayor, que es en el apoyo C: Datos: b = 40 cm, h = 60 cm, rd = 6,5 cm, d = h – rd = 60 – 6,5 = 53,5cm. 1. Dado que f’c = 280 kg/cm2 , 𝛽1 = 0,85 2. Se determina el porcentaje de acero para la sección controlada por tracción: 0,005 = t 𝜌𝑡 = 0,319 ∙ 𝛽1 ∙ 𝑓′ 𝑐 𝑓𝑦 = 0,319 ∙ 0,85 ∙ 280 4200 = 0,01808 Se diseña para un porcentaje de acero seleccionado: 𝜌 = 𝜌𝑠𝑒𝑙𝑒𝑐𝑐𝑖𝑜𝑛𝑎𝑑𝑜 = 0,90 ∙ 𝜌𝑡 = 0,90 ∙ 0,01808 = 0,0163 3. Se determina el factor de resistencia nominal R.
- 12. 𝑅 = 𝜌 · 𝑓𝑦 ∙ (1 − 0,59 ∙ 𝜌 ∙ 𝑓𝑦 𝑓′ 𝑐 ) = 0,0163 ∙ 4200 ∙ (1 − 0,59 ∙ 0,0163 ∙ 4200 280 ) 𝑅 = 58,584 𝑘𝑔 𝑐𝑚2 4. Se determina la altura útil requerida para la sección controlada por tracción: Mu = 31079,53 kgf -m 𝑑 𝑟𝑒𝑞𝑢𝑒𝑟𝑖𝑑𝑎 = √ 𝑀 𝑢 𝜙∙𝑅∙𝑏 = √ 31079,53∙100 0,90∙58,584∙40 = 38,39 cm d = 53,5 cm > 38,39 cm, se diseña como SSA. 5. Se determina para la d conocida, la cuantía mecánica específica , resolviendo la ecuación cuadrática que resulta de: 𝑀 𝑢 𝜙 ∙ 𝑓′ 𝑐 ∙ 𝑏 ∙ 𝑑2 = 𝜔(1 − 0,59 ∙ 𝜔) 31079,53 ∙ 100 0,90 ∙ 280 ∙ 40 ∙ 53,52 = 𝜔 − 0,59 ∙ 𝜔2 0,59 ∙ 𝜔2 − 𝜔 + 0,10772 = 0 La solución es = 0,1156, 6. Se determina la cuantía geométrica del acero : 𝜌 = 𝜔 ∙ 𝑓′ 𝑐 𝑓𝑦 = 0,1156 ∙ 280 4200 = 0,0077 7. Se determina el área de acero As: 𝐴 𝑠 = 𝜌 ∙ 𝑏 ∙ 𝑑 = 0,0077 ∙ 40 ∙ 53,5 = 16,48 𝑐𝑚2 8. Se determina el acero mínimo: 𝐴𝑠 𝑚𝑖𝑛 = 14 𝑓𝑦 ∙ 𝑏 ∙ 𝑑 𝑠𝑖 𝑓′ 𝑐 < 315 𝑘𝑔 𝑐𝑚2
- 13. 𝐴𝑠 𝑚𝑖𝑛 = 14 4200 ∙ 40 ∙ 53,5 = 7,13 𝑐𝑚2 𝐴 𝑠 = 16,48 𝑐𝑚2 > 7,13 𝑐𝑚2 , cumple. Para el centro del tramo: Como el momento en el tramo tiene un valor cercano al del apoyo C, se considera válido el mismo diseño de acero longitudinal por flexión. Detalle de la sección en el apoyo: Se distribuye el área de acero longitudinal por torsión Al = 10,55 cm2 en tres partes, en la parte central de la sección de la viga se colocan 2 barras de 5/8 “, y en la zona a tensión y a compresión se agregan (10,55 – 3,96)/2 = 3,295 cm2. El acero a colocar en el apoyo, en la zona traccionada (arriba) es 16,48 + 3.295 =19,78 cm2. Lo cual se suple con 4 #8, con un área de 20,27 cm2. As(abajo) = 10,13 + 3,295 =13,43 cm2 Se coloca 2 # 8 + 1 # 7 = 10,13 + 3,88 = 14,01 cm2
- 14. Diseño por torsión del lado AB: Como se cumple que 𝑻 𝒖 ≤ 𝝓 ∙ 𝟎, 𝟐𝟕 ∙ √ 𝒇′ 𝒄 ∙ 𝑨 𝒄𝒑 𝟐 𝑷 𝒄𝒑 se considera la torsión Se calcula el acero transversal por torsión: 𝐴 𝑡 𝑠 = 𝑇𝑢 𝜙⁄ 2 ∙ 𝐴 𝑜 ∙ 𝑓𝑦𝑣 ∙ 𝑐𝑡𝑔 𝜃 Asumiendo θ = 45°, Ao = 0.85·Aoh = 0.85·1581= 1343,85 cm2 𝐴 𝑡 𝑠 = 3676,2·100 0.75⁄ 2∙1343,85∙4200∙𝑐𝑡𝑔 45° = 0,0434 cm^2/cm Entonces 2𝐴 𝑡 𝑠 = 2 ∙ 0,0434 = 0,0868 cm^2/cm Se calcula el acero transversal por cortante: Se chequea si 𝑉𝑢 ≥ 𝜙 ∙ 𝑉𝑐 : Se calcula ϕ·Vc = 𝜙 · 0,53 · √𝑓′𝑐 · 𝑏 𝑤 · 𝑑 = 0,75 · 0,53 · √280 · 40 · 53,5 = 𝜙·Vc = 14234,097 kgf Como Vu = 25128,83 kgf es mayor que 𝜙Vc = 14234,097 kgf , se requiere acero transversal por corte, se calcula el acero transversal por corte: Se calcula Vs = 𝑉 𝑢 𝑐𝑟𝑖𝑡−𝜙𝑉𝑐 𝜙 = 25128,83−14234,097 0,75 = 14526,3107 kgf Se chequea con Vsmax = 2.1 · √𝑓′𝑐 · 𝑏 𝑤 · 𝑑 = 2.1 · √280 · 40 · 53,5 = 𝑉𝑠𝑚𝑎𝑥 = 75199,0032 kgf Como Vs es menor que Vsmax , se continua con el diseño, no se requiere aumentar la sección. Calcula el acero necesario por cortante: 𝐴 𝑣 𝑠 = 𝑉𝑢 𝜙⁄ −𝑉𝑐 𝑓𝑦𝑣·𝑑 = 25128,83 0,75⁄ −14234,097 0,75⁄ 4200·53,5 = 0,065 cm^2/cm Se compara con Av / s min = 0.20·√𝑓′𝑐·𝑏 𝑤 𝑓𝑦𝑣 ≥ 3.5·𝑏 𝑤 𝑓𝑦𝑣
- 15. 𝐴 𝑣 𝑠 min = 0,20·√280·40 4200 = 0,032 cm^2/cm 3,5·40 4200 = 0,0333 cm^2/cm Se debe colocar 𝐴 𝑣 𝑠 = 0,065 cm2 /cm Considerando torsión + corte, se calcula el acero transversal total: 𝐴 𝑣𝑡 𝑠 = 𝐴 𝑣 𝑠 + 2 · 𝐴 𝑡 𝑠 = 0,065 + 0,0868 = 0,1518 cm2/cm Se chequea que 𝐴 𝑣𝑡 𝑠 ≥ 3,5·𝑏 𝑤 𝑓𝑦𝑣 ⟹ se cumple 0,1518 > 0,0333 Se asume el área de estribos como # 4 de dos ramas: Av = 2·1,27 = 2,54 cm2 = 𝑠 = á𝑟𝑒𝑎 𝑑𝑒 𝑙𝑎𝑠 𝑑𝑜𝑠 𝑟𝑎𝑚𝑎𝑠 𝐴 𝑣𝑡 𝑠⁄ = 2,54 0,1518 = 16,73 cm Se calculan las separaciones máximas para torsión y para cortante y se coloca la más exigente: Por torsión 𝑠 𝑚𝑎𝑥 𝑡𝑜𝑟𝑠𝑖ó𝑛 =≤ {𝑃ℎ 8⁄ ; 30 𝑐𝑚} = {164 8⁄ = 20,5 𝑐𝑚 ; 30 𝑐𝑚} = 20,5 𝑐𝑚 Por cortante: Se chequea si Vs es menor que 1,06 · √𝑓′𝑐 · 𝑏 𝑤 · 𝑑 = 37957,5921 kgf Se cumple, entonces smax = d/2 o 60 cm (Para ND1) 𝑠 𝑚𝑎𝑥 𝑐𝑜𝑟𝑡𝑒 =≤ {0,5 · 𝑑 ; 60 𝑐𝑚; 5 · 𝐴 𝑣𝑡 · 𝑓𝑦𝑣 𝑏 𝑤 · √𝑓′𝑐 ; 𝐴 𝑣𝑡 · 𝑓𝑦𝑣 3,5 · 𝑏 𝑤 } = 𝑠 𝑚𝑎𝑥 𝑐𝑜𝑟𝑡𝑒 =≤ {0,5 · 53,5 ; 60 𝑐𝑚; 5 · 2,54 · 4200 40 · √280 ; 2,54 · 4200 3,5 · 40 } = 0,5·53,5 = 26,75 cm 5·2,54·4200 40·√280 = 79,69 cm 2,54·4200 3,5·40 = 76,20 cm
- 16. Separación elegida es : s = 16 cm. El primer estribo se colocará a 5 cm de la cara del apoyo, y los estribos siguientes a cada 16 cm, hasta donde sea necesario. El refuerzo por torsión deja de ser necesario en el punto donde 𝑻 𝒖 = 𝝓 ∙ 𝟎, 𝟐𝟕 ∙ √ 𝒇′ 𝒄 ∙ 𝑨 𝒄𝒑 𝟐 𝑷 𝒄𝒑 = 𝟎, 𝟕𝟓 ∙ 𝟎, 𝟐𝟕 ∙ √𝟐𝟖𝟎 ∙ 𝟐𝟒𝟎𝟎 𝟐 𝟐𝟎𝟎 = = 975,88 kgf·m Como en cualquier punto de la viga, el momento de torsión Tu es mayor que este valor del umbral de torsión, entonces se requiere refuerzo por torsión en toda la viga. Hacemos una tabla para considerar el efecto de las variaciones en Vu y Tu, en las separaciones de los estribos: x (m) Vu Tu 2At/s Av/s 2At/s + Av/s s (cm) 0,785 25128,83 3676,2 0,0868 0,0646 0,15149117 16,7666538 1 23389,222 3676,2 0,0868 0,0543 0,14116862 17,9926674 1,5 19343,622 3676,2 0,0868 0,0303 0,11716268 21,6792574 1,9 16107,142 3676,2 0,0868 0,0111 0,09795794 25,9294965 2,13 14246,166 3676,2 0,0868 0,0001 0,08691521 29,2238845 3 7206,822 3676,2 0,0868 0,0333 0,12014359 21,1413688 3,89 5,654 3676,2 0,0868 0,0000 0,08684359 29,2479839 Se tiene que 0,5 𝜙Vc = 7117 kgf. Observe en la tabla que el punto donde Vu tiene el valor de 𝜙Vc = 14234,097 kgf, es aproximadamente en x = 2,13 m, el punto donde Vu es igual a 0,5 𝜙Vc, es aproximadamente en x = 3 m, entre estos dos puntos la norma manda colocar refuerzo transversal mínimo por cortantes dado por 0,0333 cm2 /cm, por esto la separación en esta región se puede considerar igual a la separación máxima por cortante 20 cm. Desde x = 1,5 m hasta x = 2,13 m se coloca separación máxima por torsión igual a 20 cm. Desde x = 3 m hasta x = (7 – 2,62) =4,38 m medidos desde A, no se requiere refuerzo por cortante (Para ND1), por lo tanto en esa región se coloca el refuerzo por torsión con su separación máxima igual a 20 cm. Se colocaran estribos cerrados #4, el primero a 5 cm desde la cara de apoyo, luego 8 estribos a cada 16 cm hasta una distancia de 1,58 m desde el eje del apoyo A. Luego 13 estribos a cada 20 cm, con lo cual se llega hasta una distancia de 4,18 m, porque en x = 4,38 m ya está colocado (justo a 0,20 m más) el último estribo que viene de la parte BC, que está a x = 2,62 m de C. En total 22 estribos
- 17. como refuerzo transversal por corte y torsión, para esta parte AB. En total para la viga completa serán 41 estribos. Se calcula ahora el acero longitudinal. Se tiene 𝐴 𝑡 𝑠 = 3676,2·100 0.75⁄ 2∙1343,85∙4200∙𝑐𝑡𝑔 45° = 0,0434 cm^2/cm 𝑨𝒍 = ( 𝑨𝒕 𝒔 ) · 𝒑 𝒉 · ( 𝒇 𝒚𝒗 𝒇 𝒚𝒍 ) · 𝑪𝒕𝒈 𝟐 𝜽 ≥ 𝟏, 𝟑𝟑 · √𝒇′ 𝒄 · 𝑨 𝒄𝒑 𝒇 𝒚𝒍 − ( 𝑨𝒕 𝒔 ) · 𝒑 𝒉 · ( 𝒇 𝒚𝒗 𝒇 𝒚𝒍 ) 𝑨𝒍 = (𝟎, 𝟎𝟒𝟑𝟒) · 𝟏𝟔𝟒 · (𝟏) · 𝟏 𝟐 = 7,12 cm^2 Para calcular el Al min, At/s no debe ser menor que 1,75bw / fy =1,75·40/4200 =0,017, cumple: 𝟏,𝟑𝟑·√𝟐𝟖𝟎·𝟐𝟒𝟎𝟎 𝟒𝟐𝟎𝟎 − (𝟎. 𝟎𝟔𝟒𝟑) · 𝟏𝟔𝟒 · (𝟏) = 2,1720324 cm^2 Se cumple con Al > Al mín. Si se divide Ph entre los 30 cm de separación máxima que deben tener entre sí las barras de refuerzo longitudinal por torsión, se obtiene aproximadamente el número de barras necesarias. No. Barras = 164 / 30 = 5,47 , se consideran 6 barras. El diámetro debe ser mayor que 0,042·s = 0,042·16 =0,672 cm, pero no menor que la #3, es decir el diámetro =(3/8)·2,54 =0,953 cm. Consideremos 6 barras: el área de una barra será aproximadamente: 7,12 / 6 = 1,19 cm2 , lo cual se satisface con barras #4, con área Ab= 1,27 cm2 . Diseño por flexión de la sección rectangular: 40 x 60: Momento flexionante: En máximo en el apoyo A: 𝑀𝐴 = 30168,1 𝑘𝑔𝑓 − 𝑚 Se determina el acero para el apoyo en A: Datos: b = 40 cm, h = 60 cm, rd = 6,5 cm, d = h – rd = 60 – 6,5 = 53,5cm. 1. Dado que f’c = 280 kg/cm2 , 𝛽1 = 0,85
- 18. 2. Se determina el porcentaje de acero para la sección controlada por tracción: 0,005 = t 𝜌𝑡 = 0,319 ∙ 𝛽1 ∙ 𝑓′ 𝑐 𝑓𝑦 = 0,319 ∙ 0,85 ∙ 280 4200 = 0,01808 Se diseña para un porcentaje de acero seleccionado: 𝜌 = 𝜌𝑠𝑒𝑙𝑒𝑐𝑐𝑖𝑜𝑛𝑎𝑑𝑜 = 0,90 ∙ 𝜌𝑡 = 0,90 ∙ 0,01808 = 0,0163 3. Se determina el factor de resistencia nominal R. 𝑅 = 𝜌 · 𝑓𝑦 ∙ (1 − 0,59 ∙ 𝜌 ∙ 𝑓𝑦 𝑓′ 𝑐 ) = 0,0163 ∙ 4200 ∙ (1 − 0,59 ∙ 0,0163 ∙ 4200 280 ) 𝑅 = 58,584 𝑘𝑔 𝑐𝑚2 4. Se determina la altura útil requerida para la sección controlada por tracción: Mu = 30168,1 kgf -m 𝑑 𝑟𝑒𝑞𝑢𝑒𝑟𝑖𝑑𝑎 = √ 𝑀 𝑢 𝜙∙𝑅∙𝑏 = √ 30168,1∙100 0,90∙58,584∙40 = 37,82 cm d = 53,5 cm > 37,82 cm, se diseña como SSA. 5. Se determina para la d conocida, la cuantía mecánica específica , resolviendo la ecuación cuadrática que resulta de: 𝑀 𝑢 𝜙 ∙ 𝑓′ 𝑐 ∙ 𝑏 ∙ 𝑑2 = 𝜔(1 − 0,59 ∙ 𝜔) 30168,1 ∙ 100 0,90 ∙ 280 ∙ 40 ∙ 53,52 = 𝜔 − 0,59 ∙ 𝜔2 0,59 ∙ 𝜔2 − 𝜔 + 0,1046 = 0 La solución es = 0,112, 6. Se determina la cuantía geométrica del acero :
- 19. 𝜌 = 𝜔 ∙ 𝑓′ 𝑐 𝑓𝑦 = 0,112 ∙ 280 4200 = 0,00747 7. Se determina el área de acero As: 𝐴 𝑠 = 𝜌 ∙ 𝑏 ∙ 𝑑 = 0,00747 ∙ 40 ∙ 53,5 = 15,99 𝑐𝑚2 8. Se determina el acero mínimo: 𝐴𝑠 𝑚𝑖𝑛 = 14 𝑓𝑦 ∙ 𝑏 ∙ 𝑑 𝑠𝑖 𝑓′ 𝑐 < 315 𝑘𝑔 𝑐𝑚2 𝐴𝑠 𝑚𝑖𝑛 = 14 4200 ∙ 40 ∙ 53,5 = 7,13 𝑐𝑚2 𝐴 𝑠 = 15,99 𝑐𝑚2 > 7,13 𝑐𝑚2 , cumple. Detalle de la sección en el apoyo A: Se distribuye el área de acero longitudinal por torsión Al = 7,12 cm2 en tres partes, en la parte central de la sección de la viga se colocan 2 barras de 1/2 “, y en la zona a tensión y a compresión se agregan (7,12 – 2,53)/2 = 2,295 cm2. El acero a colocar en el apoyo, en la zona traccionada (arriba) es 15,99 + 2,295 =18,29 cm2. Lo cual se suple con 2 #8 + 3 #6, con un área de 18,68 cm2. As(abajo) = 10,13 + 2,295 =12,43 cm2 Se coloca 2 # 8 + 1 # 6 = 10,13 + 2,85 = 12,98 cm2
- 20. Detalle de la sección en el tramo: En el centro del tramo el refuerzo transversal por torsión es estribo #4 a cada 20 cm: 𝑨𝒍 = ( 𝟏,𝟐𝟕 𝟐𝟎 ) · 𝟏𝟔𝟒 · (𝟏) · 𝟏 𝟐 = 10,414 cm^2 Se distribuye el área de acero longitudinal por torsión Al = 10,414 cm2 en tres partes, en la parte central de la sección de la viga se colocan 2 barras de 5/8 “, y en la zona a tensión y a compresión se agregan (10,414 – 3,96)/2 = 3,227 cm2. El acero a colocar en el tramo, en la zona traccionada (abajo) es 16,48 + 3,227 =19,71 cm2. Lo cual se suple con 4 #8, con un área de 20,27 cm2. As(arriba) = 10,13 + 3,295 =13,43 cm2 Se coloca 2 # 8 + 1 # 7 = 10,13 + 3,88 = 14,01 cm2
