Funksioni
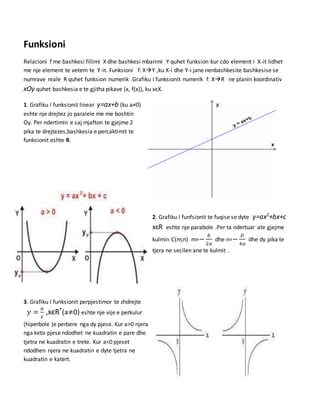
- 1. Funksioni Relacioni f me bashkesi fillimi X dhe bashkesi mbarimi Y quhet funksion kur cdo element i X-it lidhet me nje element te vetem te Y-it. Funksioni f: XY ,ku X-i dhe Y-i jane nenbashkesite bashkesise se numrave reale R quhet funksion numerik .Grafiku I funksionit numerik f: XR ne planin koordinativ xOy quhet bashkesia e te gjitha pikave (x, f(x)), ku xєX. 1. Grafiku I funksionit linear y=ax+b (ku a≠0) eshte nje drejtez jo paralele me me boshtin Oy. Per ndertimin e saj mjafton te gjejme 2 pika te drejtezes,bashkesia e percaktimit te funksionit eshte R. 2. Grafiku I funfsionit te fuqise se dyte y=ax2 +bx+c xєR eshte nje parabole .Per ta ndertuar ate gjejme kulmin C(m;n) m=− 𝑏 2𝑎 dhe n=− 𝐷 4𝑎 dhe dy pika te tjera ne secilen ane te kulmit . 3. Grafiku I funksionit perpjestimor te zhdrejte 𝑦 = 𝑎 𝑥 ,xєR* (a≠0) eshte nje vije e perkulur (hiperbole )e perbere nga dy pjese. Kur a>0 njera nga keto pjese ndodhet ne kuadratin e pare dhe tjetra ne kuadratin e trete. Kur a<0 pjeset ndodhen njera ne kuadratin e dyte tjetra ne kuadratin e katert.
- 2. 4.Grafiku I funksionit Y=ax2 ,x𝜖R (ku aє0) eshte nje vije e perkulur (parabole) qe ka si boshte simetrie boshtin Oy dhe si kulm origjinen O. Kur a>0 kjo parabole ndodhet ne gjysme planin e siperm dhe deget e saj shkojne lart pambarimisht ;a<0 kjo parabole ndodhet ne gjysme planin e poshtem dhe degte e saj shkone poshte pambarimisht. 5.Grafiku I funksionit eksponencial Y=ax , xєR kur a>1 eshte nje vije e lemuar , ndodhet mbi boshtin Ox dhe pret boshtin Oy ne piken me koordinata (0;1). Me rritjen e abshises x,rritet dhe ordinate y e pikes. Kur a<1 eshte nje vije e lemuar , ndodhet mbi boshtin Ox dhe e prêt boshtin Oy ne piken me kooordinata (0;1). Me rritjen e abshises ordinata y e pikes zvogelohet. 6.Grafiket e funksioneve y=ax ,xєR dhe y=( 1 𝑎 )x ,xєR jane simetrike te mjeri-tjetrit kundrejt bushtit Oy.
- 3. 7.Grafiku I funksionit y= log 𝑎 𝑥 ku 0<a≠1 xє ]0,+∞[ eshte nje vije e lemuar. Grafiku eshte I vendosur ne te djathte te boshtit oy dhe e pret boshtin ox ne piken (1,0). Me rritjen e vlerave te x-it grafiku vjen duke u rritur (kur a>1) dhe duke zbritur (kur o<a<1). 8.Sinusi I x-it quhet ordinate e pikes M:sinx=yM. Sinx є R. sinx eshte pozitiv(+) ne kuadratin e pare dhe te dyte ndersa negative(-) ne kuadratin e trete dhe te katert. Eshte periodik T=2𝜋 ,eshte I kufizuar .Sin(-x)=-sinx funksioni y=sinx eshte tek ne R. 9.kosinusi I X-it quhet abshisa e pikes M:cosx=XM. Cosx єR. cosx eshte pozitiv(+) ne kuadratin e pare dhe te katert ndersa negativ(-) ne kuadratin e dyte dhe te trete.Eshte periodic T= 2𝜋 ,eshte I kufizuar. Cos(-x)=cosx funksioni y=cosx eshte cift ne R.
- 4. Funksioni logaritmik Funksion logaritmik quhet funksioni i formës y =loga x ku a > 0, a ≠ 1 dhe x > 0. Nisur nga ky përkufizim kemi njëvlershmërinë y =log 𝑎 𝑥 <=> ay = x. Për x ≠ 1 shprehja y = log1x, nuk vërtetohet. Pra, formula y = log1x është funksion vetëm në se bashkësia e fillimit është X = {1}. Po kështu do të ndodhte nëse baza është 0 apo një numër negativ. Bashkësia e përcaktimit është X = R*+, ndërsa bashkësia e vlerave F = ]–∞; +∞[ = R. Per a > 1 funksioni eshte rrites ne ] 0; +∞ [ dhe rritet nga -∞ ne +∞ kur 0 < a < 1 funksioni eshte zbrites ne ] 0; +∞ [ dhe zbret nga nga +∞ ne -∞ .Bashkesia e percaktimit E = ] 0; +∞[ Per a>1 funksioni eshte I kufizuar nga larte dhe I pakufizuar nga poshte. Per o<a<1Funksioni eshte I kufizuar nga poshte e I pakufizuar nga larte. Minimumi I funksionit eksponencial eshte x=0 ,maksimumi I funksionit logaritmik eshte x=+∞. Ky funksion e pret boshtin e abshisave ne piken (1;0). Funksioni eksponencial Funksioni i formës f(x) = ax ku a > 0 dhe a ≠ 1 quhet funksion eksponencial. Bashkësia e përcaktimit është E = R = ]–∞; +∞[, ndërsa bashkësia e vlerave është F = R*+. Në përkufizimin e dhënë për funksionin eksponencial janë përjashtuar bazat a = 1, a = 0. Është bërë për arsyen e thjeshtë se f(x) = 1x = 1 dhe f(x) = 0x = 0 janë funksione konstante. Janë përjashtuar, gjithashtu, edhe vlerat negative të a-së sepse numrat negativ nuk mund të përdoren si baza. Funksioni eksponencial eshte I kufizuar nga poshte dhe I pakufizuar nga larte. Per a>1 funksioni eshte rrites . Per 0<a<1 funksioni eshte zbrites. Minimumi I funksionit eksponencial eshte x=–∞, maksimumi I funksionit eksponencial eshte x=+∞. Ky funksion e pret boshti e ordinatave ne piken (0;1).
